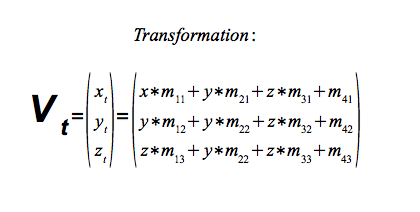Das Koordinatensystem

Es wird ein karthesisches (rechtwinkeliges) Koordinatensystem verwendet. Prinzipiell wird zwischen zwei Varianten unterschieden: Das Linkshändige Kooridinatensystem und das rechtshändige Koordinatensystem:

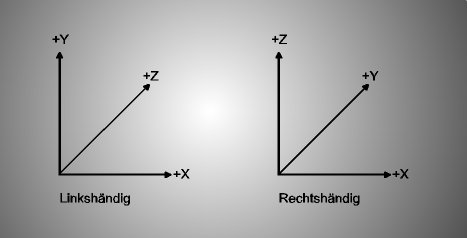
Die drei Achsen sind im Raum rechtwinkelig zueinander ausgerichtet. Im Kreuzungspunkt liegt der Ursprung. Beim linkshändigen System zeigt die Y-Achse nach oben, die X-Achse nach rechts und die Z-Achse in den Raum hinein. Je größer der Z-Wert, desto weiter entfernt liegt der Punkt vom Ursprung/Betrachter entfernt. Manchmal wird die Richtung der Z-Achse umgedreht. Dann wird der Wert kleiner, je weiter er in der Raum hineinreicht.

Beim rechtshändigen System zeigt die Z-Achse nach oben und die Y-Achse in den Raum hinein.

Es ist aber eigentlich egal, welches System man verwendet (wenn man die Wahl hat). Wichtig ist nur, das man sich konsequent daran hält. Hier wird das linkshändige Koordinatensystem verwendet.

Vektoren

Ein Vektor beschreibt einen Punkt im 3D-Raum, und weil sein Anfangspunkt im Ursprung des Koordinatensystems liegt, hat er auch eine Richtung (Richtungsvektor).

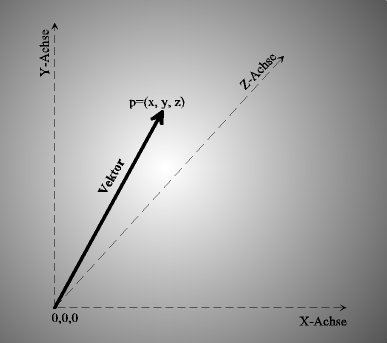
Ein Vektor ist eine Größe, die durch Betrag, Richtung und Richtungssinn bestimmt ist. Das sind typ. physikalische und technische Größen, die sich nicht durch die Angabe einer Zahl festlegen lassen. In der Physik sind das z.B. Geschwindigkeit, Feldstärke, Kraft. In der Mathematik werden sie für die Darstellung von Zahlenpaaren im Allgemeinen (z.B. bei Zahlen-n-Tupel, Matrizen) verwendet.

Größen, die im Gegensatz zu Vektoren nur durch einen Zahlenwert bestimmt sind, heißen Skalare.

In dem hier beschriebenen Kontext werden Vektoren für die Beschreibung von Koordinaten, bzw. Punkten im 3D-Raum verwendet. Formal kann ein Vektor aus n-Tupeln bestehen. Im 3D-Raum reichen drei Zahlenwerte aus, um einen Punkt zu beschreiben. Sie werden analog zum verwendeten Koordinatensystem x,y,z genannt.

Bei einfachen geometrischen Objekten, z.B. einem Würfel kann man dazu die acht Eckpunkte nehmen. Zieht man nun gedanklich eine Gerade vom Ursprung des Koordinatensystems zu jedem der Punkte, erhält man die Vektoren. Dadurch wird die Geometrie, als auch die Lage im Raum vollständig beschrieben.

Einheitsvektor

Ein Vektor vom Betrag 1 heißt Einheitsvektor. Jeder Vektor kann als Produkt aus seinem Betrag und einem Einheistvektor dargestellt werden.

Umgekehrt erhült man den Einheitsvektor indem die xyz-Komponenten durch den Betrag dividiert werden, wobei der Betrag != 0 sein muss. Die Bildung eines Einheitsvektors nennt man auch Normieren des Vektors.

Mit Vektoren kann man natürlich rechnen. Die wichtigsten Operationen sind:

Addition (und Subtraktion)

Bei der Addition werden die korrespondierenden Komponenten addiert, bzw. bei der Vektorsubtraktion subtrahiert.

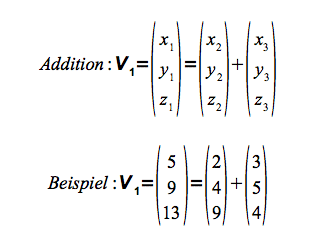
Multiplikation

Bei der Multiplikation werden die korrespondierenden Komponenten miteinander multipliziert.

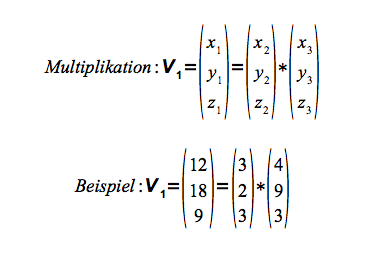
Multiplikation mit einem Skalar

Die xyz-Komponenten werden mit einer Zahl (Skalar) multipliziert.

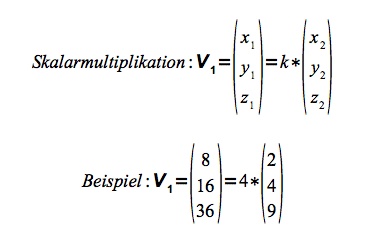
Skalarprodukt

Das Skalarprodukt (inneres Produkt) zweier Vektoren wird auch Punktprodukt oder Dot product genannt

• Wenn zwei Vektoren senkrecht aufeinander stehen, hat ihr skalares Produkt den Wert 0
• Wenn zwei Vektoren parallel zueinander liegen, hat ihr skalares Produkt den Wert |1|

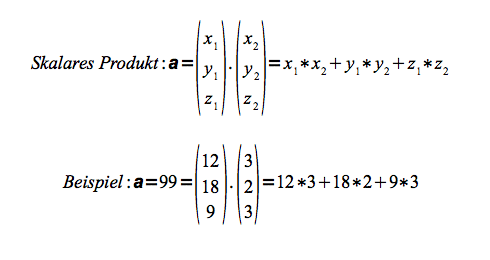
Kreuzprodukt

Das Kreuzprodukt (äusseres Produkt) zweier Vektoren wird auch Vektorprodukt genannt.

• Der Vektor v0 steht senkrecht auf der von den Vektoren v1 und v2 gebildeten Fläche.
• Der Betrag von v0 ist der Wert für die Fläche, die das von v1 und v2 aufgespannte Parallelogramm bildet.

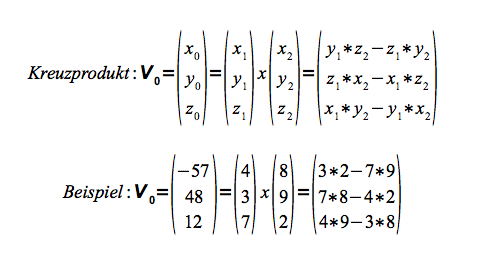
Betrag eines Vektors

Der Betrag, bzw. die Länge eines Vektors wird durch die Anwendung des Lehrsatzes von Pythargoras berechnet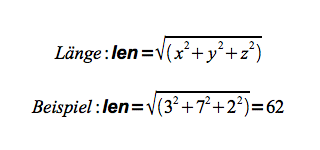

Rotation um die X-Achse

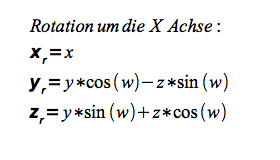
Rotation um die Y-Achse

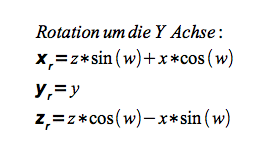
Rotation um die Z-Achse

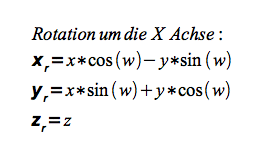
Matrizen

Um lineare Beziehungen einfach und elegant darstellen zu können, werden Matrizen verwendet. Eine Matrix ist ein rechteckig angeordnetes Schema von m * n Größen (m Zeilen, n Spalten)

Darstellung einer Matrix:

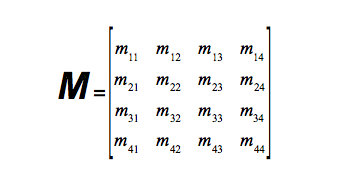
Eine Matrix mit nur einer Zeile oder Spalte heißt Vektor.

Einheitsmatrix

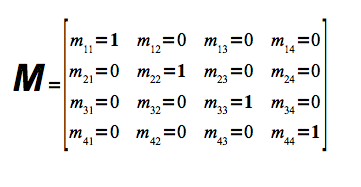
Translation

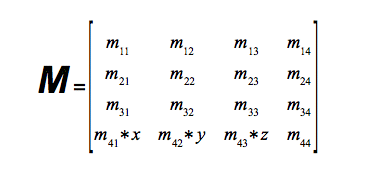
Skalierung

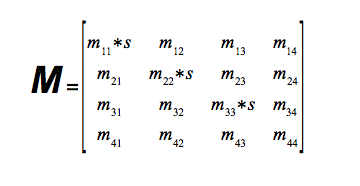
Rotation um die X Achse

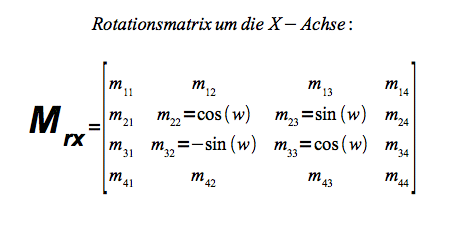
Rotation um die Y Achse

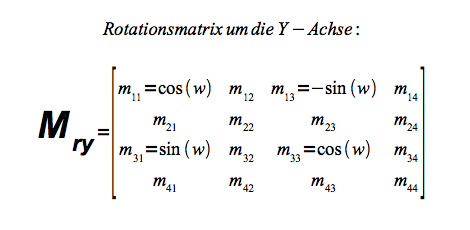
Rotation um die Z Achse

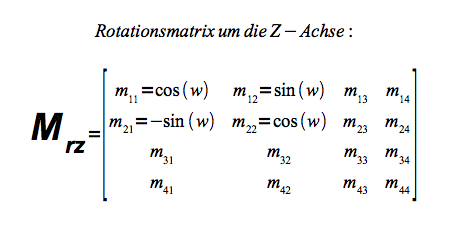
Transformation