Die Ebene (Plane)

Eigenschaften einer Ebene:

• Die Fläche einer Ebene ist unendlich groß
• Die Ebene ist unendlich dünn
• Aufgespannt wird die Ebene durch zwei beliebige Vektoren, die jedoch nicht parallel sein dürfen.

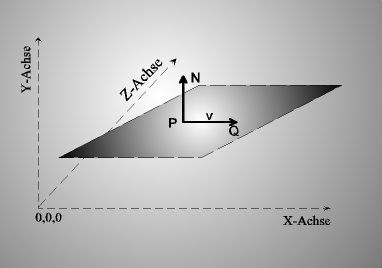
Mathematische Beschreibung:

Normalenform der Ebene: V * N + d = 0

Das * ist das Punktprodukt zweier Vektoren

Wobei gilt:

• V - Vektor in/auf der Ebene
• N - Normalenvektor der Ebene
• d - Abstand vom Nullpunkt

Die Ebene trennt den Raum in zwei Teile, d.h. es gibt eine Vorder- und eine Rückseite. Um beide auseinander zu halten verwendet man den Normalenvektor. Wenn also ein beliebiger Vektor Vi in die Formel eingesetzt wird, gelten folgende Aussagen:

Vi * N + d = 0	Vi liegt in der Ebene
Vi * N + d < 0	Vi liegt hinter der Ebene
Vi * N + d > 0	Vi liegt vor der Ebene

Die Ebene ist ein interessantes Gebilde. Damit kann man ein Frustum konstruieren oder entscheiden ob ein Polygon sichtbar ist oder nicht.

Polygone

Ein Polygon besteht aus einer Menge von Punkten im Raum. Verbindet man diese Punkte nacheinander erhält man eine Fläche.
Prinzipiell gibt es zwei Arten von Polygonen:

Für eine 3D-Engine muß man aber folgendes beachten:

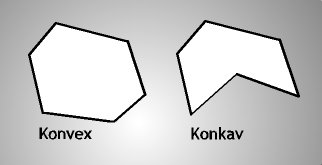
Das Polygon muß immer konvex sein. Das liegt daran, das sonst bestimmte Operationen zu kompliziert werden (z.B. Polygonclipping). Kompliziert bedeutet hier: rechenintensiv und damit inperformant. Und das ist immer ein no Go für eine 3D-Engine. Ausserdem kann ein konvexes Polygon viel einfacher in Dreiecke aufgeteilt werden.

Das Polygon muß immer in einer Ebene liegen. Weil die einzelnen Polygonpunkte im Raum liegen, kann man gekrümmte Polygone, bzw. Flächen erzeugen. Aber auch damit werden nachfolgende Berechnungen zu kompliziert.

Das geometrisch einfachste Polygon, das konvex ist und auf einer Ebene liegt, ist das Dreieck. Komplexere Formen werden aus einer Vielzahl von zusammenhängenden Dreiecken (Meshes) gebildet.

Tile

Für einfache Objekte wie Wände, Decken oder Böden reichen rechteckige Polygone mit vier Eckpunkten. Positioniert man diese Tiles mehrfach hintereinander entstehen Gänge und Räume mit beliebiger Ausdehnung.

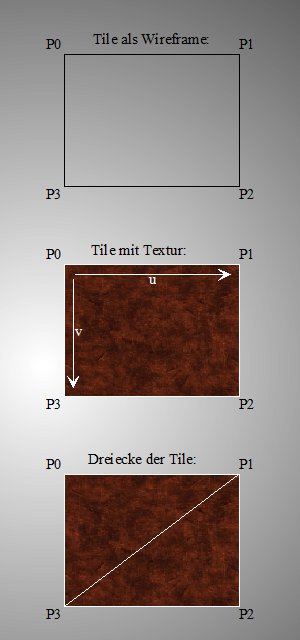Die einfachste Darstellung entsteht durch Verbindung der Eckpunkte (Wireframedarstellung) Damit die Flächen ein materielles Aussehen erhalten, wird jeder Tile eine Textur zugewiesen. Im einfachsten Falle ist das ein Bitmapdatei (GIF, PNG, BMP o.ä). Die einzelnen Texturpixel werden über ihre Spalten- und Zeilenposition bestimmt. Benannt werden sie mit u und v. Um unabhängig von der tatsächlich verwendeten Texturgröße zu sein, werden die uv-Koordinaten auf 1.0 normiert. Aber auch hier erfolgt spätestens bei der Projektion die Zerlegung in Dreiecke.